21 2101 2101 exp(iπ)+11+1=0=2 aa feafhea faf ehfaifhoeaf afeafhefa efafheaofhe a feaief
21
To be announced. Just random test...
hello world blabla...
Σ={1,…,m}N πf(x)=3+7+15+1+292+…11111={exp((x−a)(x−b)1)0x∈(a,b)⊂Rotherwise 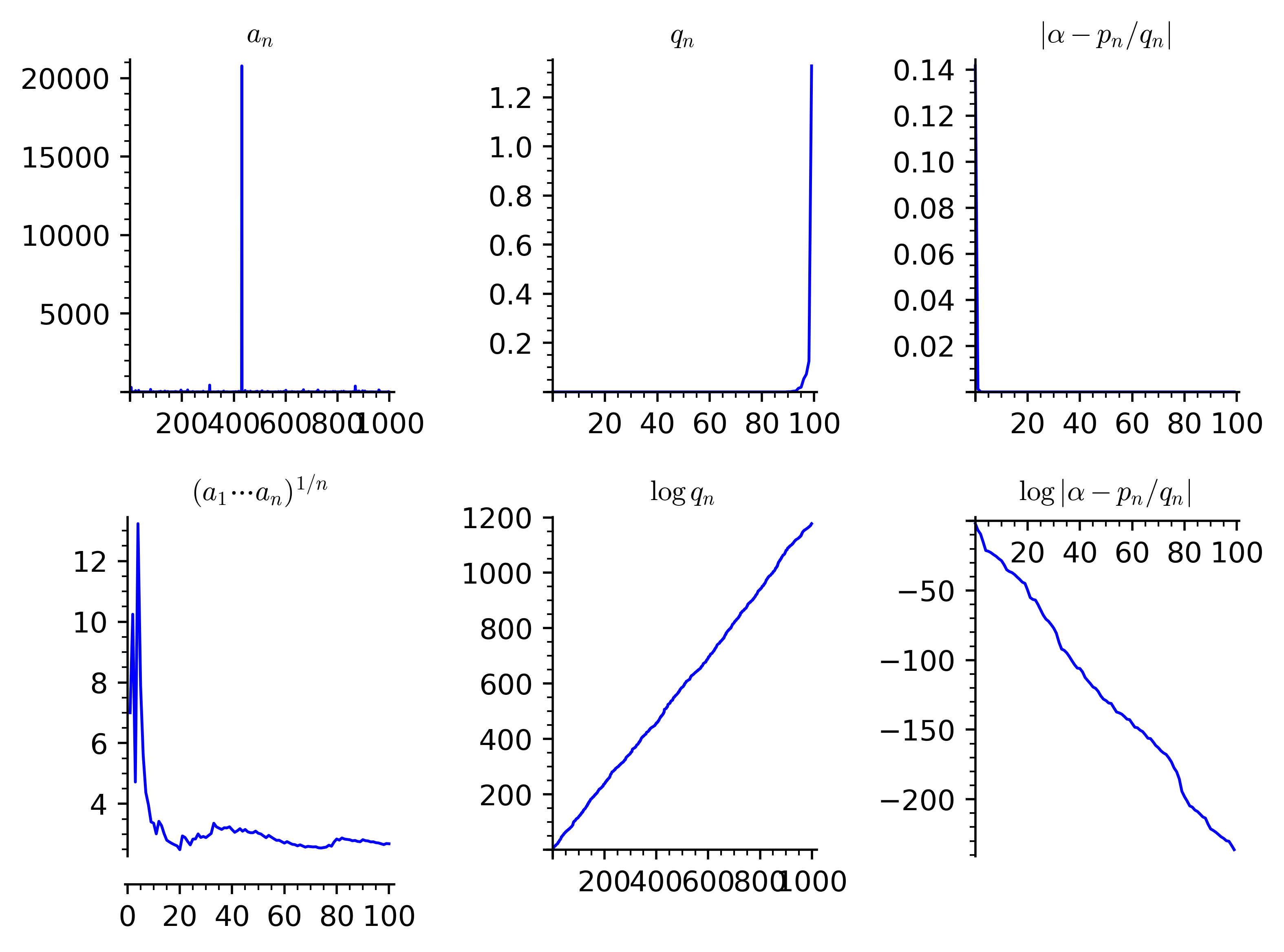 Fig 1: continued fraction of Pi
Fig 1: continued fraction of Pi Let (X,B,μ,T) be a measure-preserving system.
To be announced. Just random test...
hello world blabla...
Σ={1,…,m}N πf(x)=3+7+15+1+292+…11111={exp((x−a)(x−b)1)0x∈(a,b)⊂Rotherwise  Fig 1: continued fraction of Pi
Fig 1: continued fraction of Pi Let (X,B,μ,T) be a measure-preserving system.
To be announced. Just random test... hello world blabla... Σ={1,…,m}N
πf(x)=3+7+15+1+292+…11111={exp((x−a)(x−b)1)0x∈(a,b)⊂Rotherwise  Fig 1: continued fraction of Pi
Fig 1: continued fraction of Pi Let (X,B,μ,T) be a measure-preserving system. To be announced. Just random test... hello world blabla... Σ={1,…,m}N
πf(x)=3+7+15+1+292+…11111={exp((x−a)(x−b)1)0x∈(a,b)⊂Rotherwise  Fig 1: continued fraction of Pi
Fig 1: continued fraction of Pi Let (X,B,μ,T) be a measure-preserving system.




